|
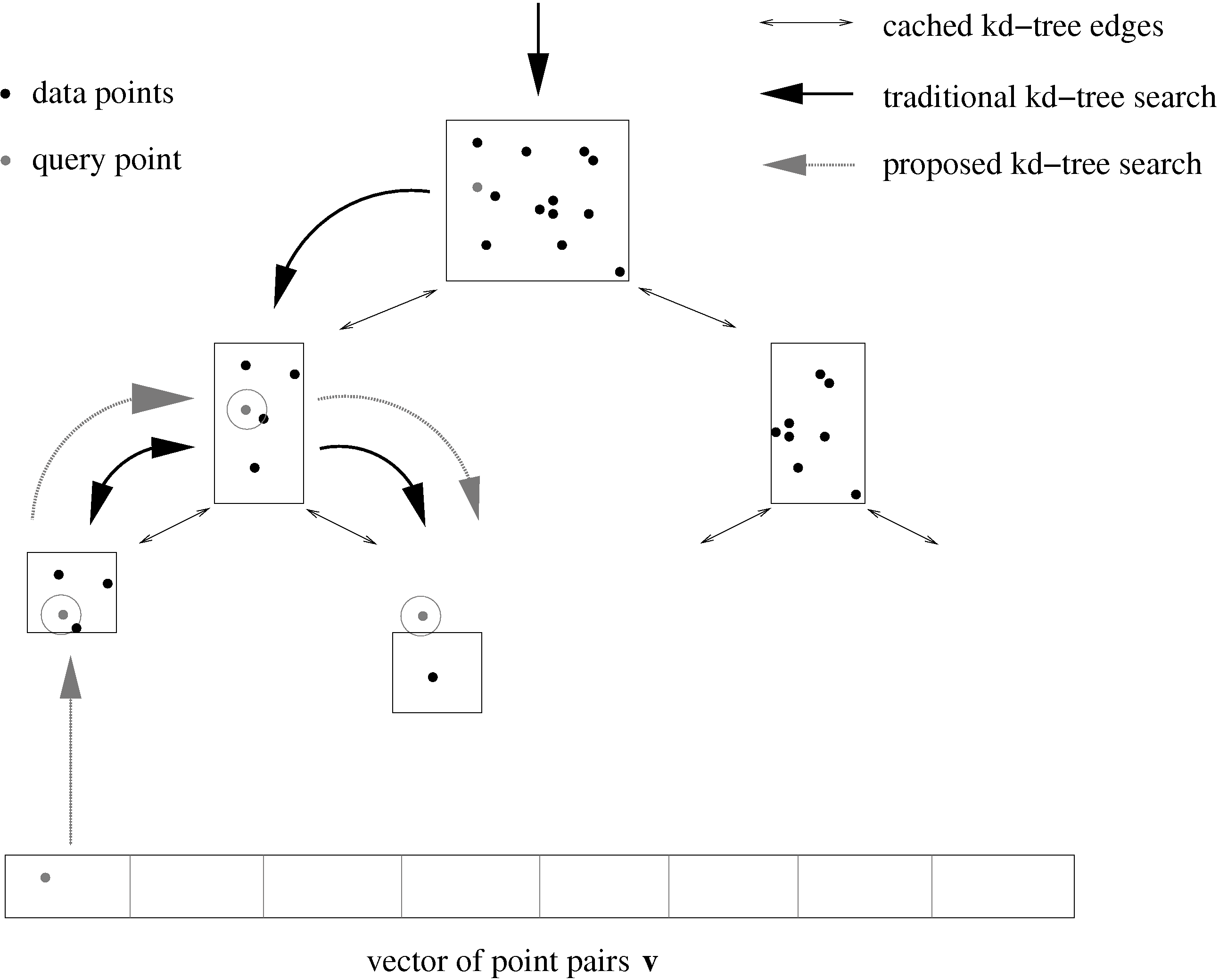
k-d trees with caching contain, in addition to the limits of the represented point set and to the two child node pointers, one pointer to the predecessor node. The root node contains a null pointer. During the recursive construction of the tree, this information is available and no extra computations are required.
For the ICP algorithm, we distinguish between the first and the following iterations: In the first iteration, a normal k-d tree search is used to compute the closest points. However, the return function of the tree is altered, such that in addition to the closest point, the pointer to the leaf containing the closest point is returned and stored in the vector of point pairs. This supplementary information forms the cache for future look-ups.

|
In the following iterations, these stored pointers are used to start the search. If the query point is located in the bucket, the bucket is searched and the ball-within-bounds test applied. Backtracking is started, iff the ball lies not completely within the bucket. If the query point is not located within the bucket, then backtracking is started, too. Since the search is started in the leaf node, explicit backtracking through the tree has to be implemented using the pointers to the predecessor nodes (see Fig. 4). Algorithm 1 summarizes the ICP with cached k-d tree search.