Next: Conclusion
Up: Cached k-d tree search for
Previous: Performance of cached k-d tree
The proposed method has been evaluated with 5 data sets from different
domains. The computation was done on a Pentium-IV with 2.8 GHz running
Linux OS, with the same compiler options, i.e., with
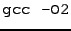 . Since k-d tree search and cached k-d tree search are very
similar, most parts of the code were identical in the comparison
experiments. In all tests, ICP with cached k-d tree search
outperformed ICP with conventional k-d tree search. Next, the detailed
results on one particular data set are described and explained. Then
we summarize the the results from the data sets.
. Since k-d tree search and cached k-d tree search are very
similar, most parts of the code were identical in the comparison
experiments. In all tests, ICP with cached k-d tree search
outperformed ICP with conventional k-d tree search. Next, the detailed
results on one particular data set are described and explained. Then
we summarize the the results from the data sets.
Table 1:
Computation times for ICP based scan registration using
standard k-d tree search vs. cached k-d tree search. The test
set differ in size and registration of scans is applied
repeatedly to construct a complete model. Illustrations of
parts of the first two and last data sets are given in
Fig. 1.
| Name of the data set |
standard k-d tree search |
cached
k-d tree search |
speedup |
| Cluttered indoor environment |
29345 ms |
12959 ms |
56% |
| Outdoor environment |
521 sec |
311 sec |
41% |
| Abandoned mine |
1112 ms |
532 ms |
52% |
| Rescue arena |
4378 ms |
2159 ms |
51% |
| Facial scans |
32 sec |
13 sec |
59% |
| Random point set |
3556 ms |
2521 ms |
29% |
The data set ``cluttered indoor environment'' was recorded during the
Rescue Robotics Camp 2004 with a 3D laser range finder that is built
on basis of a SICK scanner. A servo motor is used to achieve a
controlled pitch motion of the 2D scanner. Such 3D scanners are
commonly used in robotics. Four detailed analyses are provided:
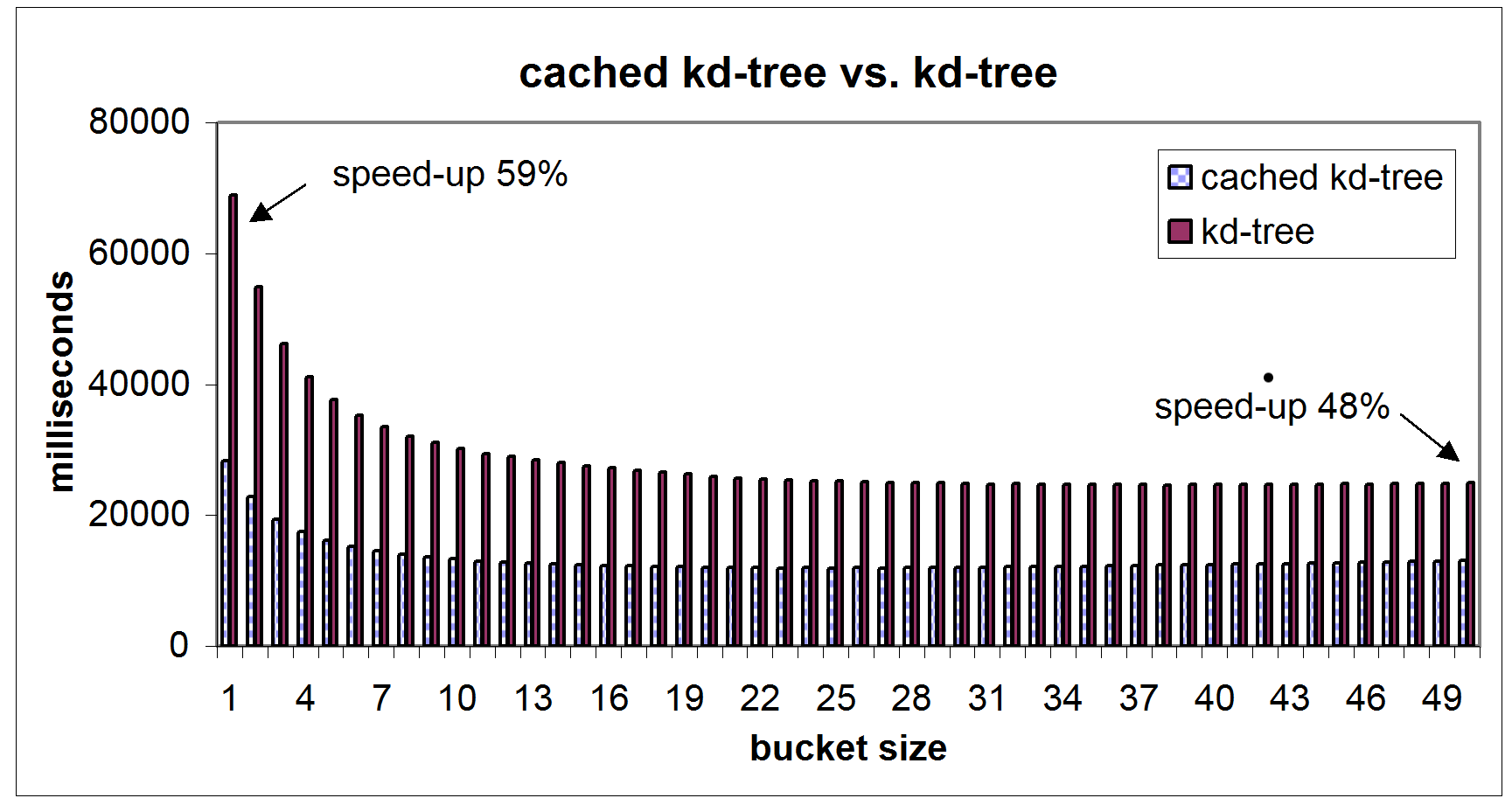
- The performance of the cached k-d tree search depending on a change
of the bucket size was tested: For small bucket sizes, the speed-up
is larger (Fig. 5, top left). This behavior
originates from the increasing time needed to search larger buckets.
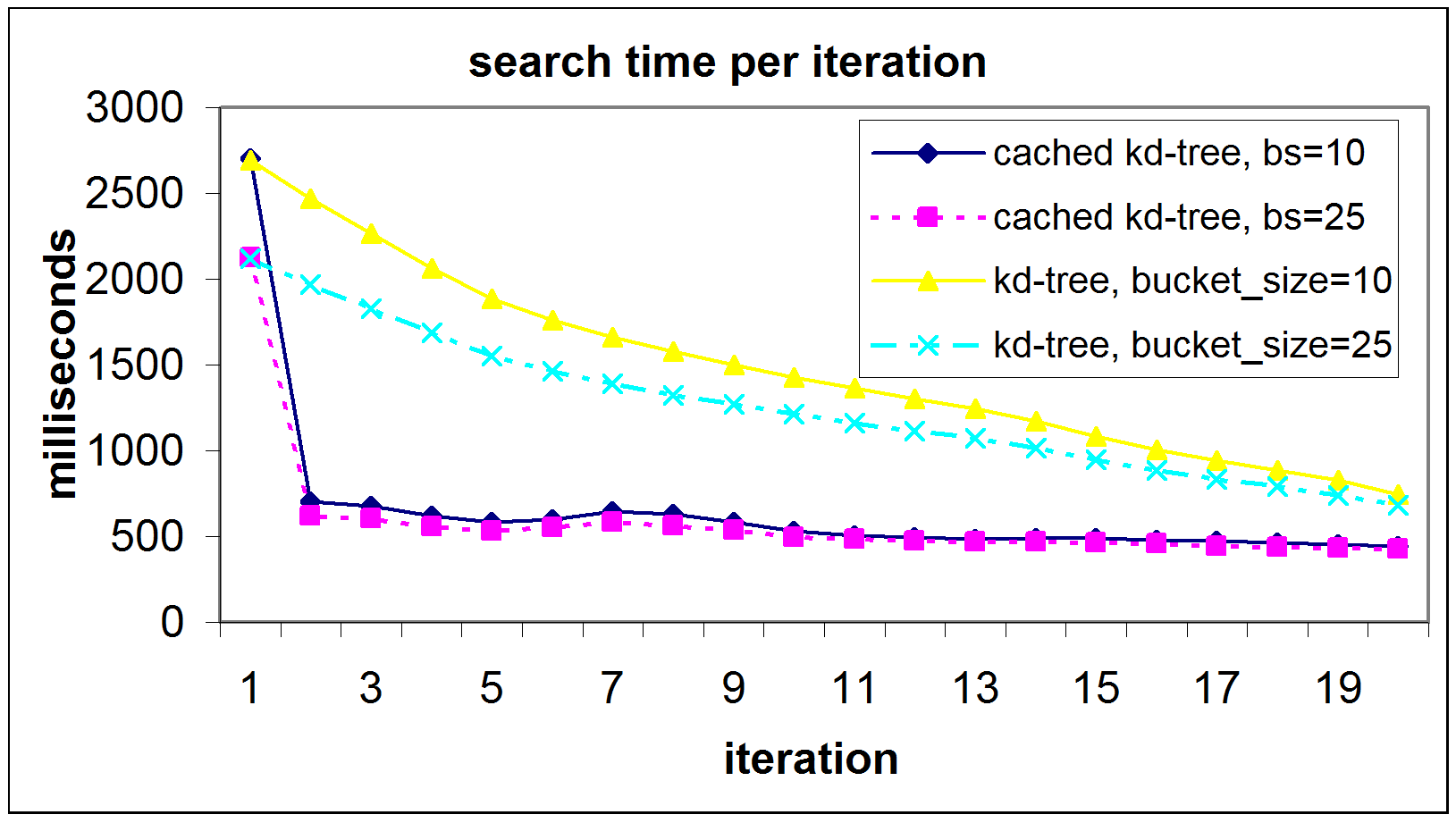
- The search time per iteration was recorded during the
experiments (Fig. 5, top right). For the first
iteration the search times are equal, since cached k-d tree
search uses conventional k-d tree search to create the cache. In
the following iterations, the search time drops significantly
and remains nearly constant. The conventional k-d tree search
increases in speed, too. Here, the amount of backtracking is
reduced due to the fact that the calculated transformations
(
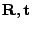 ) are getting smaller.
) are getting smaller.
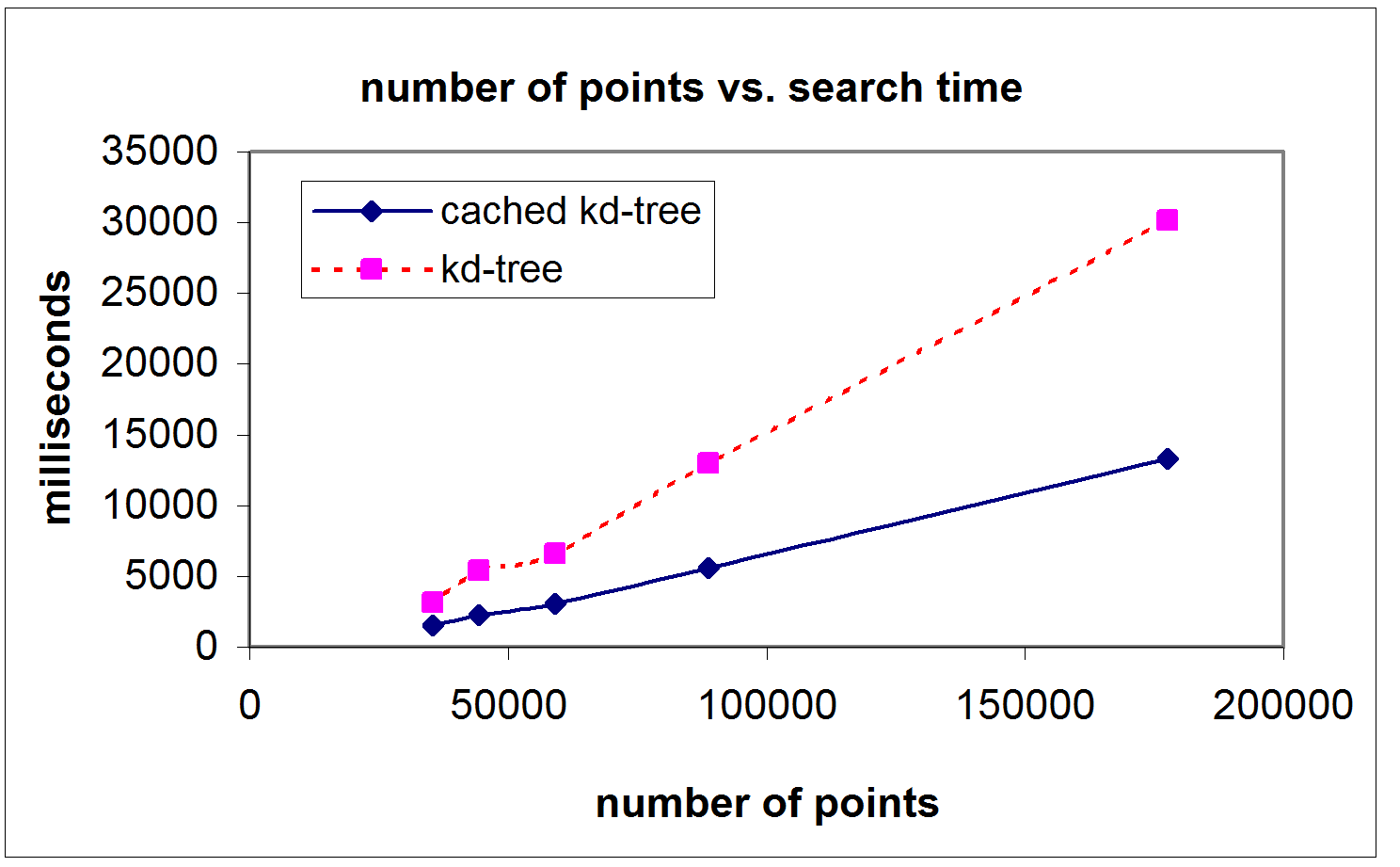
- The number of points to register influences the search time. With
increasing number of points, the positive effect of caching
algorithms becomes more and more significant
(Fig. 5, bottom left).
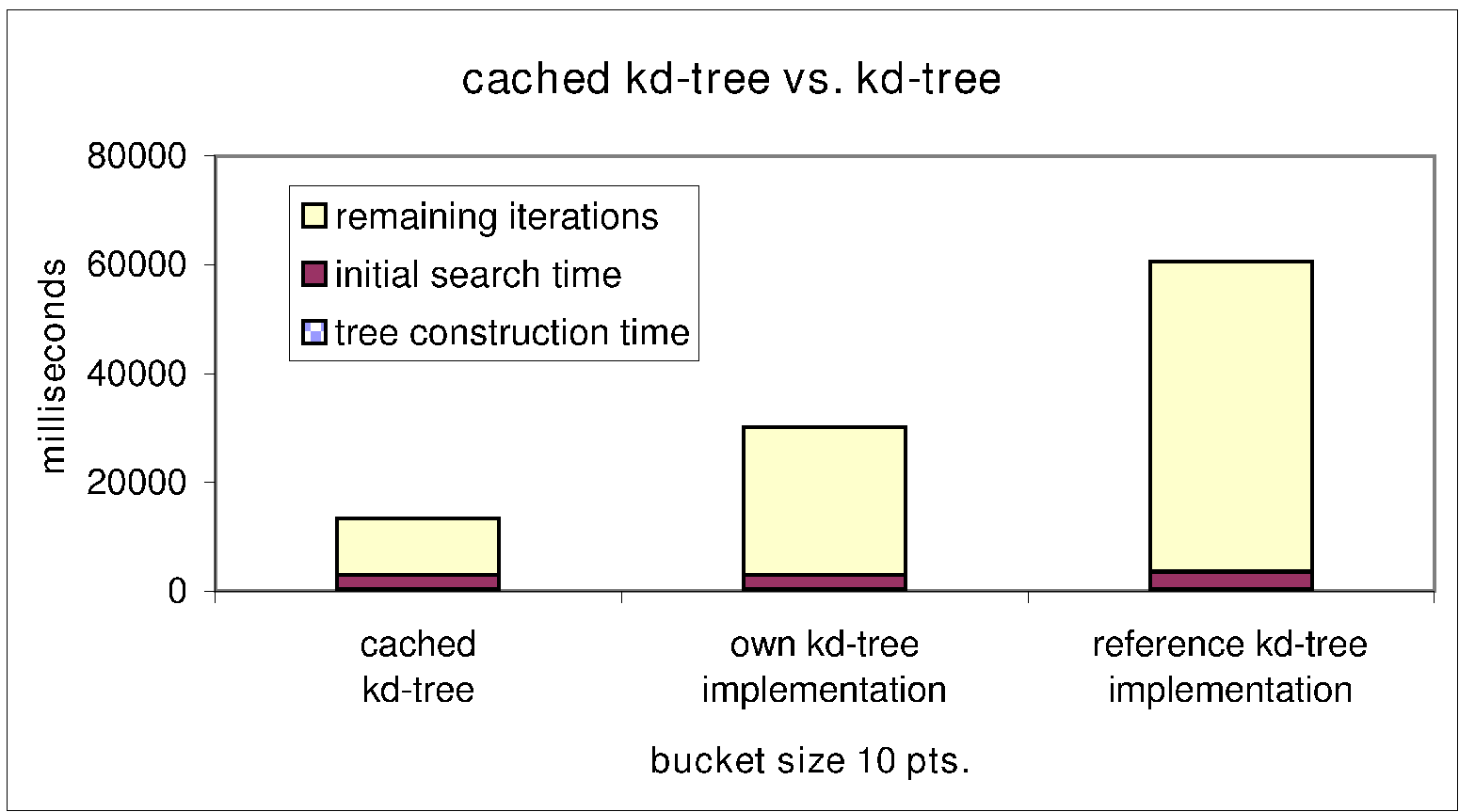
- The overall performance of the ICP algorithm depends both on the
search time and on the construction time of the tree. However, the
construction time of the trees seems to be negligible. In addition,
a comparison with a reference implementation shows the effective
implementation. As reference implementation the software from the
papers [2,3] was used (Fig. 5,
bottom right).
In addition to the detailed analysis, a number of experiments with
different data sets have been made. Table 1 summarizes
the results on different data sets originating from various ICP
applications. Overall, a speedup in the order of 50% percent is
achieved. The speedup on a point set with random points is lower,
since more cache misses occur. The reason for this effect is that ICP
aligns scans using their local structures or clusters. The cache
exploits the data conglomeration, too, but it is not present in the
random point set.
Figure 5:
Detailed results for the data set ``cluttered indoor
environment''. Top Left: search time vs. bucket size. Top right:
search time per iteration for bucket sizes 10 and 25. Bottom left:
Search time depending on the number of points. Bottom right: Overall
comparison of the algorithms and a reference k-d tree
implementation [2,3].
|
|



Next: Conclusion
Up: Cached k-d tree search for
Previous: Performance of cached k-d tree
root
2007-05-31
![]() . Since k-d tree search and cached k-d tree search are very
similar, most parts of the code were identical in the comparison
experiments. In all tests, ICP with cached k-d tree search
outperformed ICP with conventional k-d tree search. Next, the detailed
results on one particular data set are described and explained. Then
we summarize the the results from the data sets.
. Since k-d tree search and cached k-d tree search are very
similar, most parts of the code were identical in the comparison
experiments. In all tests, ICP with cached k-d tree search
outperformed ICP with conventional k-d tree search. Next, the detailed
results on one particular data set are described and explained. Then
we summarize the the results from the data sets.