The above recursion can be used for proving a lower bound.
![]()
Assume the claim was false, and there was a ![]() -competitive
strategy for
-competitive
strategy for
![]() .
We show that
.
We show that
![]() holds,
making it impossible for the robot to get further than a distance
of
holds,
making it impossible for the robot to get further than a distance
of ![]() away from the start, a contradiction.
Clearly, we have
away from the start, a contradiction.
Clearly, we have
![]() for step 1.
Moreover,
for step 1.
Moreover,
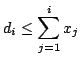
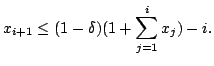
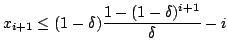 |
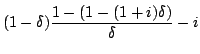 |
||
Instead of increasing the distance ![]() we could as well
consider a situation where start and corner are a distance 1 apart, but the
scan cost is only
we could as well
consider a situation where start and corner are a distance 1 apart, but the
scan cost is only ![]() . Now Theorem 1
shows a remarkable discontinuity: Even for a scan cost arbitrarily small,
a lower bound of 2 cannot be beaten, whereas for zero scan cost, a factor
of
. Now Theorem 1
shows a remarkable discontinuity: Even for a scan cost arbitrarily small,
a lower bound of 2 cannot be beaten, whereas for zero scan cost, a factor
of
![]() can be obtained [9].
can be obtained [9].
On the positive side, for ![]() intermediate scan points, Equation (1)
provides
intermediate scan points, Equation (1)
provides ![]() optimality conditions. As there are
optimality conditions. As there are ![]() degrees
of freedom (the coordinates of intermediate scan points),
we get an underdetermined nonlinear optimization problem for any given
distance
degrees
of freedom (the coordinates of intermediate scan points),
we get an underdetermined nonlinear optimization problem for any given
distance ![]() , provided that we know the number of scan points.
For
, provided that we know the number of scan points.
For ![]() , this can be used to derive an optimal competitive factor of
1.808201..., achieved with one intermediate scan point.
For larger
, this can be used to derive an optimal competitive factor of
1.808201..., achieved with one intermediate scan point.
For larger ![]() (and hence, larger
(and hence, larger ![]() ) one could derive additional
geometric optimality conditions and use them in combination with more
complex numerical methods.
However, this approach appears impractical for real applications,
for reasons stated above. As we will see in the following, there is
a better approach.
) one could derive additional
geometric optimality conditions and use them in combination with more
complex numerical methods.
However, this approach appears impractical for real applications,
for reasons stated above. As we will see in the following, there is
a better approach.
ARRAY(0x93985d0)