


Next: Approximate box decomposition trees
Up: Closest Point Search
Previous: The optimized k-d tree
S. Arya and D. Mount introduce the following notion for approximating
the nearest neighbor in k-d trees [2]: Given an
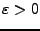 , then the point
, then the point
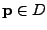 is the
is the
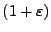 -approximate
nearest neighbor of the point
-approximate
nearest neighbor of the point
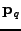 , iff
, iff
where
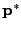 denotes the true nearest neighbor, i.e.,
denotes the true nearest neighbor, i.e.,
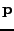 has a maximal distance of
has a maximal distance of
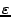 to the true nearest
neighbor. Using this notation, in every step the algorithm
records the closest point
to the true nearest
neighbor. Using this notation, in every step the algorithm
records the closest point
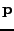 . The search terminates if the
distance to the unanalyzed leaves is larger than
Fig. 3 (left) shows an example where the gray
cell needs not to be analyzed, since the point
. The search terminates if the
distance to the unanalyzed leaves is larger than
Fig. 3 (left) shows an example where the gray
cell needs not to be analyzed, since the point
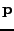 satisfies
the approximation criterion.
satisfies
the approximation criterion.
root
2007-05-31
![]() , then the point
, then the point
![]() is the
is the
![]() -approximate
nearest neighbor of the point
-approximate
nearest neighbor of the point
![]() , iff
, iff