|
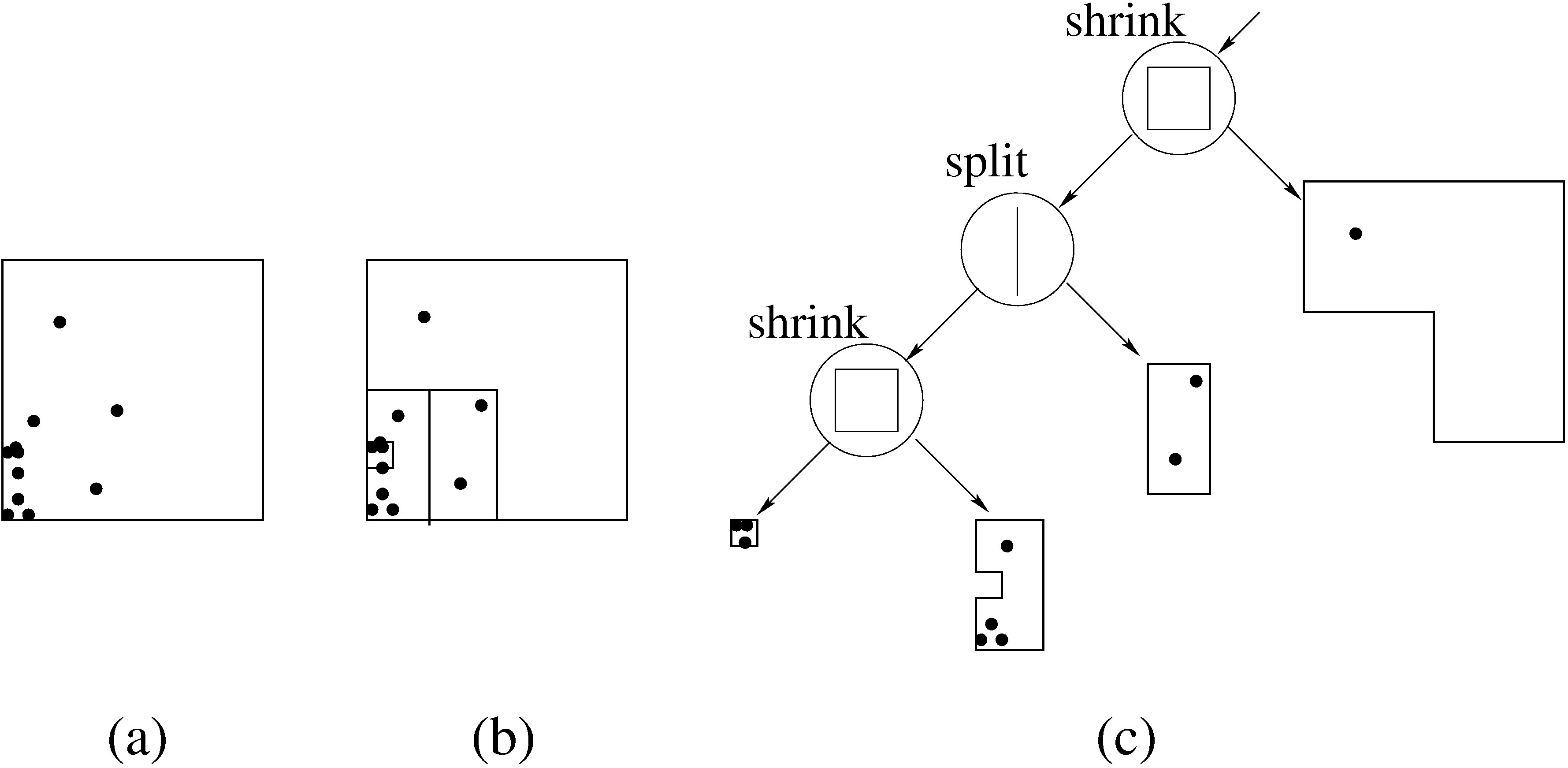
Arya et al. have presented an algorithm for approximate nearest neighbor search and proved its optimality [3]. They use a balanced box decomposition tree (bd-tree) as their primary data structure. This tree combines two important properties of geometric data structures: First, as in the k-d tree case, the set of points is exponentially reduced. Second, the aspect ratio of the tree edges is bounded by a constant. Not even the optimized k-d tree is able to make this assurance, but quadtrees show this characteristic [3]. The actual box decomposition search tree is composed of splits and shrinks. Fig. 3 (c) shows the general structure.


|
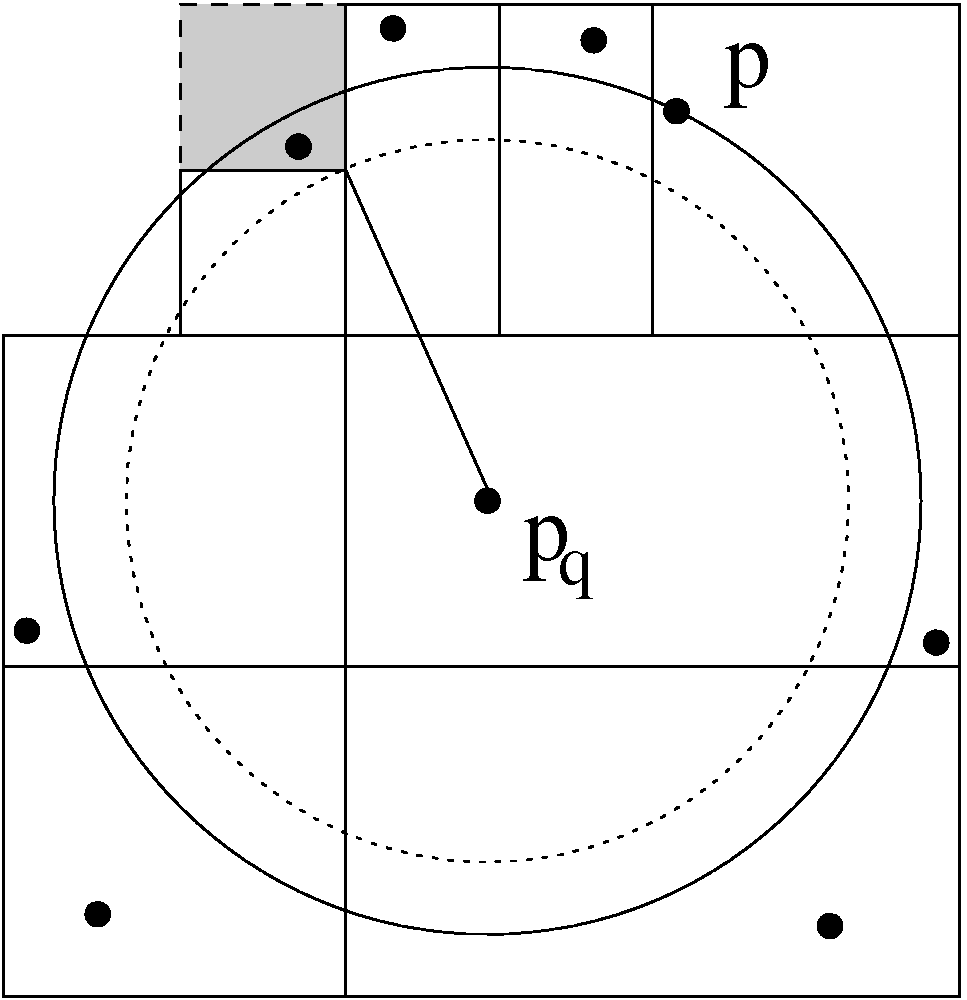
The search procedure of bd-trees is similar to the one of approximate k-d trees. The approximate search is discontinued (cf. Fig. 3) if the distance to the unanalyzed leaves is larger than