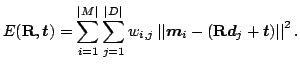 |
(1) |
![]() is assigned 1 if the
is assigned 1 if the ![]() -th point of
-th point of ![]() describes the
same point in space as the
describes the
same point in space as the ![]() -th point of
-th point of ![]() . Otherwise
. Otherwise
![]() is 0. Two things have to be calculated: First, the
corresponding points, and second, the transformation (
is 0. Two things have to be calculated: First, the
corresponding points, and second, the transformation (![]() ,
, ![]() ) that minimizes
) that minimizes
![]() on the base of the
corresponding points.
on the base of the
corresponding points.
The ICP algorithm calculates iteratively the point
correspondences. In each iteration step, the algorithm selects
the closest points as correspondences and calculates the
transformation (
![]() ) for minimizing equation
(1). The assumption is that in the last iteration step
the point correspondences are correct. Besl et al. prove that
the method terminates in a minimum [4]. However,
this theorem does not hold in our case, since we use a maximum
tolerable distance
) for minimizing equation
(1). The assumption is that in the last iteration step
the point correspondences are correct. Besl et al. prove that
the method terminates in a minimum [4]. However,
this theorem does not hold in our case, since we use a maximum
tolerable distance
![]() max for associating the scan
data. Such a threshold is required though, given that 3D scans
overlap only partially.
max for associating the scan
data. Such a threshold is required though, given that 3D scans
overlap only partially.
In every iteration, the optimal transformation (![]() ,
, ![]() )
has to be computed. Eq. (1) can be reduced to
)
has to be computed. Eq. (1) can be reduced to
with
![]() , since the
correspondence matrix can be represented by a vector containing
the point pairs.
, since the
correspondence matrix can be represented by a vector containing
the point pairs.
Four direct methods are known to minimize eq. (2)
[14]. In earlier work
[19,24,25] we used a quaternion based
method [4], but the following one, based on singular
value decomposition (SVD), is robust and easy to implement, thus
we give a brief overview of the SVD-based algorithm. It was first
published by Arun, Huang and Blostein [2]. The
difficulty of this minimization problem is to enforce the
orthonormality of the matrix ![]() . The first step of the
computation is to decouple the calculation of the rotation
. The first step of the
computation is to decouple the calculation of the rotation ![]() from the translation
from the translation ![]() using the centroids of the points
belonging to the matching, i.e.,
using the centroids of the points
belonging to the matching, i.e.,
The registration calculates the optimal rotation by
![]() . Hereby, the matrices
. Hereby, the matrices ![]() and
and ![]() are derived by the
singular value decomposition
are derived by the
singular value decomposition
![]() of a
correlation matrix
of a
correlation matrix ![]() . This
. This
![]() matrix
matrix ![]() is
given by
is
given by
We have proposed and evaluated algorithms to accelerate ICP, namely
point reduction and approximate ![]() d-trees
[19,24,25]. They are used here, too.
d-trees
[19,24,25]. They are used here, too.