


Next: Herleitung der Formel für
Up: Das Quaternion zur Darstellung
Previous: Das Quaternion zur Darstellung
Berechnung der Rotationsmatrix aus dem Einheitsquaternion
Jedes Quaternion kann durch eine
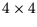 Matrix repräsentiert
werden. Sei das Quaternion
Matrix repräsentiert
werden. Sei das Quaternion
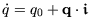 mit
mit
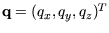 , dann wird eine Matrix
, dann wird eine Matrix
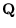 wie folgt definiert:
wie folgt definiert:
 |
|
|
(7.7) |
mit
Die Schreibweise eines Quaternions als Matrix stellt eine
bijektive Abbildung zwischen der Menge der Quaternionen und der
Menge der
 Matrizen der Form (A.7) dar. Wie
folgender Satz zeigt, entspricht die Multiplikation von Matrizen
der Form (A.7) jener von Quaternionen.
Matrizen der Form (A.7) dar. Wie
folgender Satz zeigt, entspricht die Multiplikation von Matrizen
der Form (A.7) jener von Quaternionen.
Satz 5
Seien
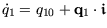
und
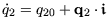
zwei Quaternionen und
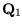
und
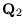
die
zugehörigen Matrix-Darstellungen. Wenn
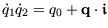
ist, dann gilt:
Beweis:Bezeichne
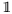 die
die
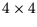 Einheitsmatrix. Damit gilt:
Einheitsmatrix. Damit gilt:
Es folgt:
Sei
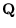 die Matrix-Darstellung des Quaternions
die Matrix-Darstellung des Quaternions
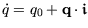 . Aus der Definition der Matrix-Darstellung wird ersichtlich,
dass die Matrix-Repräsentation von
. Aus der Definition der Matrix-Darstellung wird ersichtlich,
dass die Matrix-Repräsentation von 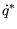 gerade die transponierte
Matrix
gerade die transponierte
Matrix
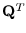 ist. Interessant ist die folgende Beziehung:
ist. Interessant ist die folgende Beziehung:
Aus diesem Grund ist die Matrix
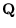 immer orthogonal, wenn
immer orthogonal, wenn
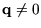 ist. Speziell für ein Einheitsquaternion gilt folgender Satz:
ist. Speziell für ein Einheitsquaternion gilt folgender Satz:
Satz 6
Für ein Einheitsquaternion
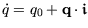
ist die
zugehörige Matrix
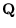
eine
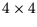
Rotationsmatrix, d.h. es gilt:
Beweis:Für ein Einheitsquaternion gilt:
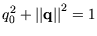 . Nach
(A.7) ist
. Nach
(A.7) ist
und somit
Wegen
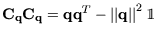 ergibt sich:
ergibt sich:
Der zweite Teil des Satzes wird mit Hilfe des Laplaceschen
Entwicklungssatzes [21] bewiesen:
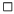
Definiert man für ein Quaternion
 die Matrix
die Matrix
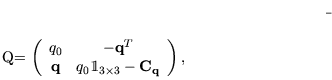 |
|
|
(7.8) |
erhält man ähnliche Eigenschaften wie für
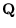 aus Definition
(A.7). Wenn
aus Definition
(A.7). Wenn 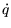 ein Einheitsquaternion ist, dann stellt
auch
ein Einheitsquaternion ist, dann stellt
auch
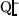 eine Rotationsmatrix im 4-dimensionalen Raum dar und
es gilt
eine Rotationsmatrix im 4-dimensionalen Raum dar und
es gilt
Unterabschnitte



Next: Herleitung der Formel für
Up: Das Quaternion zur Darstellung
Previous: Das Quaternion zur Darstellung
Andreas Nüchter
2002-07-10
![]() Matrix repräsentiert
werden. Sei das Quaternion
Matrix repräsentiert
werden. Sei das Quaternion
![]() mit
mit
![]() , dann wird eine Matrix
, dann wird eine Matrix
![]() wie folgt definiert:
wie folgt definiert:
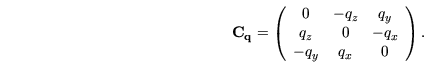
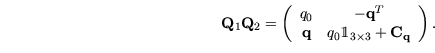
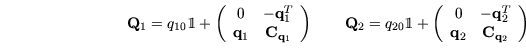
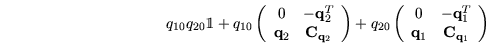
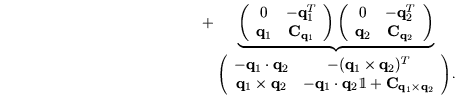
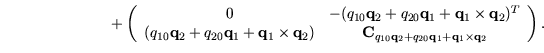
![]() die Matrix-Darstellung des Quaternions
die Matrix-Darstellung des Quaternions
![]() . Aus der Definition der Matrix-Darstellung wird ersichtlich,
dass die Matrix-Repräsentation von
. Aus der Definition der Matrix-Darstellung wird ersichtlich,
dass die Matrix-Repräsentation von ![]() gerade die transponierte
Matrix
gerade die transponierte
Matrix
![]() ist. Interessant ist die folgende Beziehung:
ist. Interessant ist die folgende Beziehung:
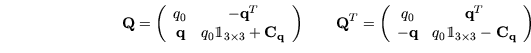
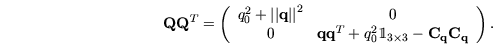
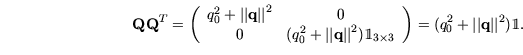

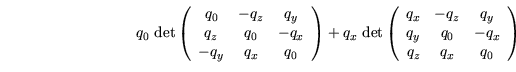
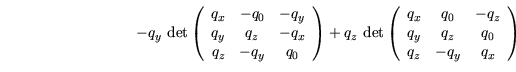
![]() die Matrix
die Matrix