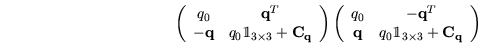 |
|||
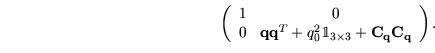 |
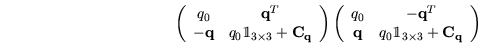 |
|||
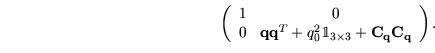 |
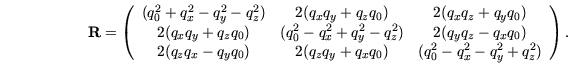 |
Die Matrixdarstellung
![]() eines Quaternions erlaubt eine effiziente
Schreibweise der Multiplikation. Das Produkt zweier Quaternionen lässt
sich als Matrix-Vektor-Produkt schreiben, wenn mit einem
Quaternion
eines Quaternions erlaubt eine effiziente
Schreibweise der Multiplikation. Das Produkt zweier Quaternionen lässt
sich als Matrix-Vektor-Produkt schreiben, wenn mit einem
Quaternion
![]() der Spaltenvektor
der Spaltenvektor
![]() assoziiert wird.
Damit ergeben sich
assoziiert wird.
Damit ergeben sich ![]() und
und ![]() als
als
Ein Vektor
![]() wird durch ein
Quaternion dargestellt, das ausschließlich aus einem imaginären Teil
besteht, d.h.
wird durch ein
Quaternion dargestellt, das ausschließlich aus einem imaginären Teil
besteht, d.h.
![]() .
Dadurch ist es möglich, eine Rotation durch das Hintereinanderschalten
von Multiplikationen der Quaternionen auszudrücken:
.
Dadurch ist es möglich, eine Rotation durch das Hintereinanderschalten
von Multiplikationen der Quaternionen auszudrücken:
Im nun anschließenden Abschnitt wird nachgewiesen, dass das
Einheitsquaternion
![]() mit
mit
![]() und
und
![]() tatsächlich
eine Rotation um den Winkel
tatsächlich
eine Rotation um den Winkel ![]() um den Einheitsvektor
um den Einheitsvektor
![]() darstellt (vgl. Abbildung 3.1).
darstellt (vgl. Abbildung 3.1).