


Next: Ergebnisse des Scanmatchings als
Up: Transformationsschätzung
Previous: Transformationsschätzung
Zunächst wird die Berechnung der Rotation 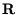 von der Berechnung der
Translation
von der Berechnung der
Translation
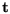 getrennt, um die Rotation separat zu bestimmen. Die
Translation findet man anschließend ausgehend von der Rotation. Eine
solche Entkopplung ist möglich, weil für eine Lösung
getrennt, um die Rotation separat zu bestimmen. Die
Translation findet man anschließend ausgehend von der Rotation. Eine
solche Entkopplung ist möglich, weil für eine Lösung
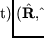 von (3.7) gilt, dass
von (3.7) gilt, dass
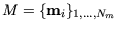 und
und
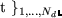 den gleichen Schwerpunkt haben.
den gleichen Schwerpunkt haben.
Der erste Schritt berechnet zwei Punktmengen 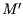 und
und 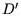 von den
Originalpunktmengen
von den
Originalpunktmengen 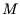 und
und 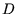 , indem von jedem Punkt der Schwerpunkt der
Punktmengen subtrahiert wird. Es ist
, indem von jedem Punkt der Schwerpunkt der
Punktmengen subtrahiert wird. Es ist
und
Die Gleichung (3.7) vereinfacht sich zu
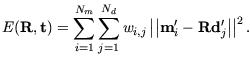 |
|
|
(3.15) |
Die Herleitung für obiges Resultat befindet sich in Anhang A.2.1.
Nachdem eine Lösung für (3.15) bestimmt ist, ergibt sich die
Translation als
Die gesuchte Rotation 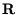 findet man mit Hilfe der
findet man mit Hilfe der
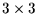 Kovarianz-Matrix
Kovarianz-Matrix
 , die sich aus den Punkten von
, die sich aus den Punkten von 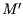 und
und 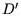 bildet:
bildet:
Diese Matrix enthält alle notwendigen Informationen, um 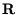 unter Benutzung der Methode der kleinsten Quadrate zu berechnen. Die
einzelnen Elemente von
unter Benutzung der Methode der kleinsten Quadrate zu berechnen. Die
einzelnen Elemente von
 bestimmen sich wie folgt:
bestimmen sich wie folgt:
mit
Eine symmetrische
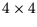 Matrix
Matrix
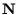 wird aus
wird aus
 berechnet:
berechnet:
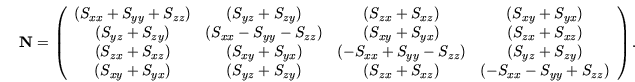 |
|
|
(3.16) |
Die Eigenvektoren und die zugehörigen Eigenwerte von
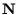 müssen
berechnet werden. Horn zeigt, dass das Einheitsquaternion
müssen
berechnet werden. Horn zeigt, dass das Einheitsquaternion
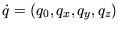 der gesuchten Rotation dem Eigenvektor des
größten positiven Eigenwertes von
der gesuchten Rotation dem Eigenvektor des
größten positiven Eigenwertes von
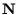 entspricht
[40]. Der Beweis für diese Tatsache findet sich in Anhang
A.2.2. Die Nullstellen des charakteristischen Polynoms
der Matrix
entspricht
[40]. Der Beweis für diese Tatsache findet sich in Anhang
A.2.2. Die Nullstellen des charakteristischen Polynoms
der Matrix
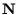 sind die gesuchten Eigenwerte. Da das Polynom den
Grad 4 hat, lassen sich die Eigenwerte direkt berechnen (Methode von
Ferrari). Die gesuchte orthonormale Rotationsmatrix berechnet man
anschließend aus dem Einheitsquaternion
sind die gesuchten Eigenwerte. Da das Polynom den
Grad 4 hat, lassen sich die Eigenwerte direkt berechnen (Methode von
Ferrari). Die gesuchte orthonormale Rotationsmatrix berechnet man
anschließend aus dem Einheitsquaternion 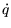 mit
(3.6).
mit
(3.6).

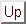


Next: Ergebnisse des Scanmatchings als
Up: Transformationsschätzung
Previous: Transformationsschätzung
Andreas Nüchter
2002-07-10
![]() und
und ![]() von den
Originalpunktmengen
von den
Originalpunktmengen ![]() und
und ![]() , indem von jedem Punkt der Schwerpunkt der
Punktmengen subtrahiert wird. Es ist
, indem von jedem Punkt der Schwerpunkt der
Punktmengen subtrahiert wird. Es ist
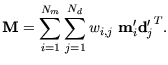
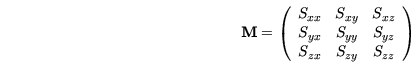
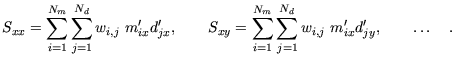
![]() müssen
berechnet werden. Horn zeigt, dass das Einheitsquaternion
müssen
berechnet werden. Horn zeigt, dass das Einheitsquaternion
![]() der gesuchten Rotation dem Eigenvektor des
größten positiven Eigenwertes von
der gesuchten Rotation dem Eigenvektor des
größten positiven Eigenwertes von
![]() entspricht
[40]. Der Beweis für diese Tatsache findet sich in Anhang
A.2.2. Die Nullstellen des charakteristischen Polynoms
der Matrix
entspricht
[40]. Der Beweis für diese Tatsache findet sich in Anhang
A.2.2. Die Nullstellen des charakteristischen Polynoms
der Matrix
![]() sind die gesuchten Eigenwerte. Da das Polynom den
Grad 4 hat, lassen sich die Eigenwerte direkt berechnen (Methode von
Ferrari). Die gesuchte orthonormale Rotationsmatrix berechnet man
anschließend aus dem Einheitsquaternion
sind die gesuchten Eigenwerte. Da das Polynom den
Grad 4 hat, lassen sich die Eigenwerte direkt berechnen (Methode von
Ferrari). Die gesuchte orthonormale Rotationsmatrix berechnet man
anschließend aus dem Einheitsquaternion ![]() mit
(3.6).
mit
(3.6).